Hypothesis Testing

Objective

To determine what the true mean, μ, is not (gather evidence of H_A).

Given

Note: This notebook is built for cases where the population is normally distributed and the population standard deviation is unknown.  This leads to the use of Student's T distribution; while this is mathematically appropriate for any sample size, the specific techniques used in this notebook are likely to result in long run times for large n.
     The use of Student's T distribution is appropriate even for non-normal distributions if n is reasonably large.  However, such use is beyond the scope of this course, and the use of this notebook under those conditions is perhaps inappropriate for computational reasons.

Definitions

Define the Student's T distribution (and load useful Mathematica packages).

f_T[x_] := Gamma[(df + 1)/2]/Gamma[df/2] * 1/(df * π)^(1/2) * (1 + x^2/df)^(-(df + 1)/2)

<<Statistics`

<<Graphics`FilledPlot`

<<Graphics`Arrow`

Check plot to ensure we have correctly entered the PDF

Plot[f_T[x], {x, -5, 5}] ;

[Graphics:../HTMLFiles/index_609.gif]

Sample Data

Sample data, if provided

sample = {1, 2, 3}

{1, 2, 3}

Sample Statistics

If sample data is provided, compute the appropriate sample statistics.  If the sample statistics are provided, enter them here.

xbar = Mean[sample]

s = StandardDeviation[sample]

n = Length[sample]

df = n - 1

2

1

3

2

Required

For the given sample data and hypothesis, compute the p-value and state the appropriate conclusion about the null and alternate hypotheses.

Computations

1.  State H_0 and H_A

Note: Pay particular attention to the direction of the inequality in H_A; an incorrect choice here will result in an inappropriate conclusion even if all of the computations are correct.

H_0 = μ= μ 0

μ_0 = 5(* μ_0 must be an actual numerical value ! *)

H_A = μ< μ 0

μ= μ 0

5

μ< μ 0

Note: The procedures below attempt to be robust to the choice of the direction of inequality.  However, if the test statistic is on the "wrong" side of μ_0 (e.g. above μ_0 when the direction of inequality for H_A is  μ<μ_o, bad things may potentially happen, especially with the pure Mathematica functions.

2.  Calculate the Test Statistic

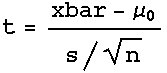
t = (xbar - μ_0)/(s/n^(1/2))

-3 3^(1/2)

3. Find the P-Value

a.  Plot the distribution of the test statistic if H_0 is true

Plot[f_T[x], {x, -6, 6}] ;

[Graphics:../HTMLFiles/index_637.gif]

b. Plot the test statistic on the number line

showSigma = 7

7

[Graphics:../HTMLFiles/index_641.gif]

Note: as you can see from the code to display it, adding the test statistic (and other modifications to the plot we will encounter shortly) are both doable in Mathematica and significantly more complex than cadets are normally expected to master.
     While this display code has been somewhat tested, it is not guaranteed to be robust.  

[Graphics:../HTMLFiles/index_643.gif]

c.  Calculate the appropriate area based on the form of H_A (one-tailed test)

pvalue = ∫_ (-∞)^(-Abs[t]) f_T[x] x

1/58 (29 - 3 87^(1/2))

WARNING: the use of  "-Abs[t]" in the integral is to ensure that we are looking at the left tail, regardless of the actual sign of t.  This exploits the symmetry of the Student's T distibution -- if you are modifying this notebook for other purposes, beware.

N[pvalue]

0.0175494

Note: the following two procedures are not taught in this course, but are provided for crosschecking of solutions by instructors.  Note that if sample data are not provided, the invocation of MeanTest will fail.

StudentTPValue[t, df, TwoSided→False]

OneSidedPValue→0.0175494

MeanTest[sample, μ_0, FullReport→True, TwoSided→False]

{FullReport→ {{Mean, TestStat, Distribution}, {2., -5.19615, StudentTDistribution[2]}}, OneSidedPValue→0.0175494}

Solution

Interpret the p-value in terms of the original problem, to include the words true mean and units.

Created by Mathematica  (July 20, 2006) Valid XHTML 1.1!