The Weibull Distribution

Probability Density Function

Define the Probability Density Function (PDF) of the random variable X by entering the function f(x) along with the lowest and highest x-values it supports.

In[90]:=

Begin["WeibullProperties`"] ;

lowsupport = 0 ;

highsupport = ∞ ;

α = 5 ;

β = 2 ;

f[x_, α_, β_] := α/β^α * x^(α - 1) * ^(-(x/β)^α)

Property 1:  Ensure f(x) ≥ 0 for all x by plotting it.

In[95]:=

Plot[f[x, α, β], {x, 0, 5}, PlotRange→ {0, 1}] ;

[Graphics:../HTMLFiles/index_419.gif]

Property 2:  Ensure f(x) integrates to exactly 1 over the random variable's support.

In[105]:=

∫_lowsupport^highsupport f[x, α, β] x

Out[105]=

1

Property 3:  P(X = c) = 0, or the probability assigned to any particular value c is zero.

Property 4:  Create the Cumulative Distribution Function (CDF).

In[129]:=

F[x_, α_, β_] = ∫_lowsupport^x f[y, α, β] y         

Out[129]=

1 - ^(-x^5/32)

Plot the CDF.

In[130]:=

Plot[F[x, α, β], {x, 0, 5}, PlotRange→ {0, 1}] ;

[Graphics:../HTMLFiles/index_425.gif]

Property 5:  Use the PDF to compute probability, where a and b are the lower and upper bounds of the interval of interest.

In[121]:=

a = 2 ;

b = 4 ;

PDFProb = ∫_a^b f[x, α, β] x ;

Print["P(", a, " ≤ X ≤ ", b, ") = ", N[PDFProb]]

P(2 ≤ X ≤ 4) = 0.367879

Property 6:  Use the CDF to compute probability.

In[131]:=

Off[General :: spell1]

CDFProb = F[b, α, β] - F[a, α, β] ;

On[General :: spell1]

Print["P(", a, " ≤ X ≤ ", b, ") = ", N[CDFProb]]

P(2 ≤ X ≤ 4) = 0.367879

Property 7:  Compute the Expected Value.

In[137]:=

ExpValue = ∫_lowsupport^highsupport x * f[x, α, β] x         

Out[137]=

2 Gamma[6/5]

In[138]:=

N[ExpValue]

Out[138]=

1.83634

Using similar methods, we find that the expected value is

In[139]:=

β * Gamma[1 + 1/α]

Out[139]=

2 Gamma[6/5]

Property 8:  Compute the Variance/Standard Deviation.

In[140]:=

Var = ∫_lowsupport^highsupport (x - ExpValue)^2 f[x, α, β] x   

Out[140]=

-4 Gamma[6/5]^2 + 4 Gamma[7/5]

In[141]:=

N[Var^(1/2)]

Out[141]=

0.420618

In[142]:=

(* Alternatively *)∫_lowsupport^highsupport x^2 f[x, α, β] x - ExpValue^2

Out[142]=

-4 Gamma[6/5]^2 + 4 Gamma[7/5]

Finally, the formula for the variance is

In[143]:=

β^2 (Gamma[1 + 2/α] - (Gamma[1 + 1/α])^2)

Out[143]=

4 (-Gamma[6/5]^2 + Gamma[7/5])

In[144]:=

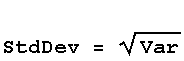
                   StdDev = Var^(1/2)

Out[144]=

(-4 Gamma[6/5]^2 + 4 Gamma[7/5])^(1/2)

Property 9:  Use the CDF to find a percentile.

NOTE: "ExpValue" simply specifies a starting value for the "FindRoot" search.  For the Weibull, the expected value is a reasonable starting point for most percentiles.

In[145]:=

p = .90 ;

FindRoot[F[xstar, α, β] == p, {xstar, ExpValue}]

Out[146]=

{xstar→2.36305}

In[147]:=

End[]

Out[147]=

WeibullProperties`

Created by Mathematica  (July 20, 2006) Valid XHTML 1.1!